

我们想要大致计算卫星相对于地面站的多普勒效应。请注意,为了进行准确的计算,包括光程延迟、对流层效应和其他因素,最好使用测量生成功能。这个例子只是作为基本教程。
一方面,让我们首先定义卫星的一些初始状态:
初始轨道只需设置为CartesianOrbit。有关轨道表示的更多详细信息可以在库架构文档的轨道部分中找到。
Frame inertialFrame = FramesFactory.getEME2000();
TimeScale utc = TimeScalesFactory.getUTC();
AbsoluteDate initialDate = new AbsoluteDate(2008, 10, 01, 0, 0, 00.000, utc);
double mu = 3.986004415e+14;
Vector3D position = new Vector3D(-6142438.668, 3492467.560, -25767.25680);
Vector3D velocity = new Vector3D(505.8479685, 942.7809215, 7435.922231);
PVCoordinates pvsat = new PVCoordinates(position, velocity);
Orbit initialOrbit = new CartesianOrbit(pvsat, inertialFrame, initialDate, mu);
作为一个传播器,我们考虑一个简单的KeplerianPropagator,它将在初始轨道所定义的惯性参考系(这里是EME2000)中传播轨道。
Propagator kepler = new KeplerianPropagator(initialOrbit);
另一方面,让我们通过其坐标在自己的TopocentricFrame中定义地面站,该地面站与某个地球参考系中的BodyShape相关联。
Frame earthFrame = FramesFactory.getITRF(IERSConventions.IERS_2010, true);
BodyShape earth = new OneAxisEllipsoid(Constants.WGS84_EARTH_EQUATORIAL_RADIUS,
Constants.WGS84_EARTH_FLATTENING,
earthFrame);
double longitude = FastMath.toRadians(45.);
double latitude = FastMath.toRadians(25.);
double altitude = 0.;
GeodeticPoint station = new GeodeticPoint(latitude, longitude, altitude);
TopocentricFrame staF = new TopocentricFrame(earth, station, "station");
有关BodyShape和GeodeticPoint的更多详细信息可以在库架构文档的bodies部分中找到。有关TopocentricFrame的更多详细信息可以在库架构文档的frames部分中找到。
最后,我们可以在一个简单的传播循环中获取多普勒测量
AbsoluteDate finalDate = initialDate.shiftedBy(6000);
AbsoluteDate extrapDate = initialDate;
while (extrapDate.compareTo(finalDate) <= 0) {
// 我们可以简单地在任何时间获取卫星在地面站参考系中的位置和速度
PVCoordinates pvInert = kepler.propagate(extrapDate).getPVCoordinates();
PVCoordinates pvStation = inertialFrame.getTransformTo(staF, extrapDate).transformPVCoordinates(pvInert);
// 然后计算多普勒信号
double doppler = Vector3D.dotProduct(pvStation.getPosition(), pvStation.getVelocity()) / pvStation.getPosition().getNorm();
System.out.format(Locale.US, "%s %9.3f%n", extrapDate, doppler);
extrapDate = extrapDate.shiftedBy(600);
}
这个程序显示的结果如下:
时间 多普勒频移 (m/s)
2008-10-01T00:00:00.000 -2925.114
2008-10-01T00:10:00.000 -3069.084
2008-10-01T00:20:00.000 -1331.910
2008-10-01T00:30:00.000 1664.611
2008-10-01T00:40:00.000 3143.549
2008-10-01T00:50:00.000 2832.906
2008-10-01T01:00:00.000 1556.662
2008-10-01T01:10:00.000 -140.889
2008-10-01T01:20:00.000 -1860.637
2008-10-01T01:30:00.000 -3195.728
2008-10-01T01:40:00.000 -3538.053
这个示例的完整代码可以在教程的源代码树中找到,文件名为src/main/java/org/orekit/tutorials/frames/Frames1.java。
该问题与库架构文档中的用户定义的参考系子部分中所述的问题相关。
可以通过以下示意图来概括该问题。
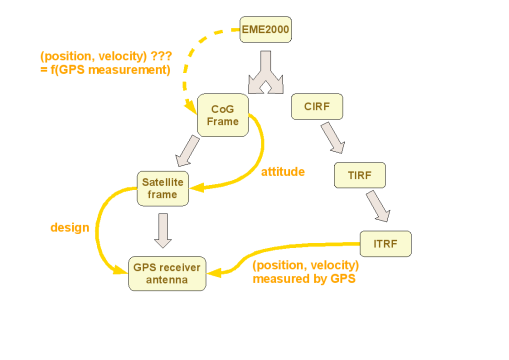
对于给定的卫星,可以在任何时刻获得以ITRF参考系表示的位置和速度的GPS测量值。GPS天线与卫星参考系有一定的偏移量。卫星参考系相对于与卫星重心相关的某个移动参考系的姿态在任何时刻都是已知的。我们想要计算某个时刻卫星重心在EME2000惯性参考系中的位置和速度。
OREKIT提供的一个可能的解决方案如上所述。
质心坐标系的原点位于卫星质心,并与EME2000对齐。它通过一个先验未知的变换与其父EME2000坐标系相连,该变换取决于当前位置和速度。我们想要计算这个变换。
首先我们构建坐标系。我们使用恒等变换作为一个简单的虚拟值,真实的值是时间相关的,将在时间重置时重新计算:
Frame cogFrame = new UpdatableFrame(FramesFactory.getEME2000(), Transform.IDENTITY, "LOF", false);
卫星坐标系,其原点也位于质心,取决于姿态。为了本教程的简单起见,我们在这里考虑一个简单的惯性姿态:
Transform cogToSat = new Transform(new Rotation(0.6, 0.48, 0, 0.64, false));
Frame satFrame = new Frame(cogFrame, cogToSat, "sat", false);
最后,GPS天线坐标系总是通过2个变换从卫星坐标系定义的:一个平移和一个旋转。让我们设置一些值:
Transform translateGPS = new Transform(new Vector3D(0, 0, 1));
Transform rotateGPS = new Transform(date,
new Rotation(new Vector3D(0, 1, 3),
FastMath.toRadians(10),
RotationConvention.VECTOR_OPERATOR));
Frame gpsFrame = new Frame(satFrame,
new Transform(date, translateGPS, rotateGPS),
"GPS", false);
让我们考虑一些在UTC时间尺度上的测量日期:
TimeScale utc = TimeScalesFactory.getUTC();
AbsoluteDate date = new AbsoluteDate(2008, 10, 01, 12, 00, 00.000, utc);
然后让我们在这一刻获取一些由GPS天线测量的卫星在ITRF中的位置和速度:
Vector3D position = new Vector3D(-6142438.668, 3492467.560, -25767.25680);
Vector3D velocity = new Vector3D(505.8479685, 942.7809215, 7435.922231);
在这一刻,从GPS坐标系到ITRF坐标系的变换由一个平移和一个旋转定义。平移直接由上述GPS测量提供。旋转从现有的树中提取,我们知道所有的旋转已经是最新的,即使一个平移仍然未知。我们通过首先应用旋转来结合提取的旋转和测量的平移,因为位置/速度向量是在ITRF坐标系中给出的,而不是在GPS天线坐标系中:
Transform measuredTranslation = new Transform(date, position, velocity);
Transform formerTransform = gpsFrame.getTransformTo(FramesFactory.getITRF(IERSConventions.IERS_2010, true), date);
Transform preservedRotation = new Transform(date,
formerTransform.getRotation(),
formerTransform.getRotationRate());
Transform gpsToItrf = new Transform(date, preservedRotation, measuredTranslation);
现在我们可以更新从EME2000到CoG坐标系的变换。
updateTransform方法会自动定位全局树中的坐标系,组合所有的变换,并更新CoG本身与其父级EME2000坐标系之间的单一变换。
cogFrame.updateTransform(gpsFrame, FramesFactory.getITRF(IERSConventions.IERS_2010, true), gpsToItrf, date);
坐标系树现在已经同步。我们可以计算所有所需的位置和速度对:
PVCoordinates origin = PVCoordinates.ZERO;
Transform cogToItrf = cogFrame.getTransformTo(FramesFactory.getITRF(IERSConventions.IERS_2010, true), date);
PVCoordinates satItrf = cogToItrf.transformPVCoordinates(origin);
Transform cogToEme2000 = cogFrame.getTransformTo(FramesFactory.getEME2000(), date);
PVCoordinates satEME2000 = cogToEme2000.transformPVCoordinates(origin);
作为结果,我们可以将GPS测量值与计算值进行比较:
GPS天线在ITRF中的位置: -6142438.668 3492467.560 -25767.257
GPS天线在ITRF中的速度: 505.8479685 942.7809215 7435.9222310
卫星在ITRF中的位置: -6142439.167 3492468.238 -25766.717
卫星在ITRF中的速度: 505.8480179 942.7809579 7435.9222310
卫星在EME2000中的位置: 6675017.354 -2317478.630 -31517.561
卫星在EME2000中的速度: -150.5212935 -532.0401727 7436.0739031
这个示例的完整代码可以在教程的源代码树中找到,文件名为src/main/java/org/orekit/tutorials/frames/Frames2.java。
假设我们有一艘航天器,其姿态由偏航控制定律引导,我们想要绘制这种定律对航天器运动的一些影响。
首先,将航天器的初始轨道定义如下:
Frame eme2000 = FramesFactory.getEME2000();
AbsoluteDate initialDate = new AbsoluteDate(2003, 4, 7, 10, 55, 21.575,
TimeScalesFactory.getUTC());
double mu = 3.986004415e+14;
Orbit orbit = new CircularOrbit(7178000.0, 0.5e-4, -0.5e-4,
FastMath.toRadians(50.),
FastMath.toRadians(220.),
FastMath.toRadians(5.300),
PositionAngleType.MEAN,
eme2000, initialDate, mu);
有关轨道表示的更多细节可以在库架构文档的轨道部分找到。
然后构建航天器的姿态控制律:
偏航控制律将法线点控制律包装起来,以便给太阳电池阵提供最大的光照,其旋转轴在航天器坐标系中为Y轴:
Frame earthFrame = FramesFactory.getITRF(IERSConventions.IERS_2010, true);
BodyShape earth = new OneAxisEllipsoid(Constants.WGS84_EARTH_EQUATORIAL_RADIUS,
Constants.WGS84_EARTH_FLATTENING,
earthFrame);
NadirPointing nadirLaw = new NadirPointing(eme2000, earth);
final PVCoordinatesProvider sun = CelestialBodyFactory.getSun();
YawSteering yawSteeringLaw = new YawSteering(eme2000, nadirLaw, sun, Vector3D.MINUS_I);
有关姿态表示的更多细节可以在库架构文档的姿态部分找到。
作为一个传播器,我们考虑使用解析的EcksteinHechlerPropagator。
Propagator propagator =
new EcksteinHechlerPropagator(orbit, yawSteeringLaw,
Constants.EIGEN5C_EARTH_EQUATORIAL_RADIUS,
Constants.EIGEN5C_EARTH_MU,
Constants.EIGEN5C_EARTH_C20,
Constants.EIGEN5C_EARTH_C30,
Constants.EIGEN5C_EARTH_C40,
Constants.EIGEN5C_EARTH_C50,
Constants.EIGEN5C_EARTH_C60);
有关Propagator的更多细节可以在库架构文档的传播部分找到。
然后,我们将一个步骤处理器与传播器关联起来,使用当前的航天器状态直接在航天器坐标系中计算所需的数据
propagator.getMultiplexer().add(10, new OrekitFixedStepHandler() {
public void init(SpacecraftState s0, AbsoluteDate t, final double step)
// 写入文件头
}
public void handleStep(SpacecraftState currentState) {
Transform inertToSpacecraft = currentState.toTransform();
Vector3D sunInert = sun.getPVCoordinates(currentState.getDate(), currentState.getFrame()).getPosition();
Vector3D sunSat = inertToSpacecraft.transformPosition(sunInert);
Vector3D spin = inertToSpacecraft.getRotationRate();
// 将数据写入文件
}
public void finish(final SpacecraftState finalState) {
// 关闭文件
}
}
因此,在一个轨道上进行计算,我们可以绘制以下结果,清楚地显示出典型的偏航转向行为:
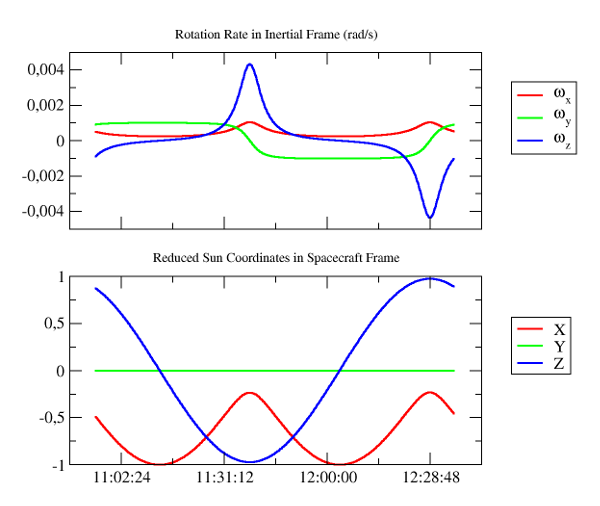
这个示例的完整代码可以在教程的源代码树中找到,文件名为src/main/java/org/orekit/tutorials/frames/Frames3.java。